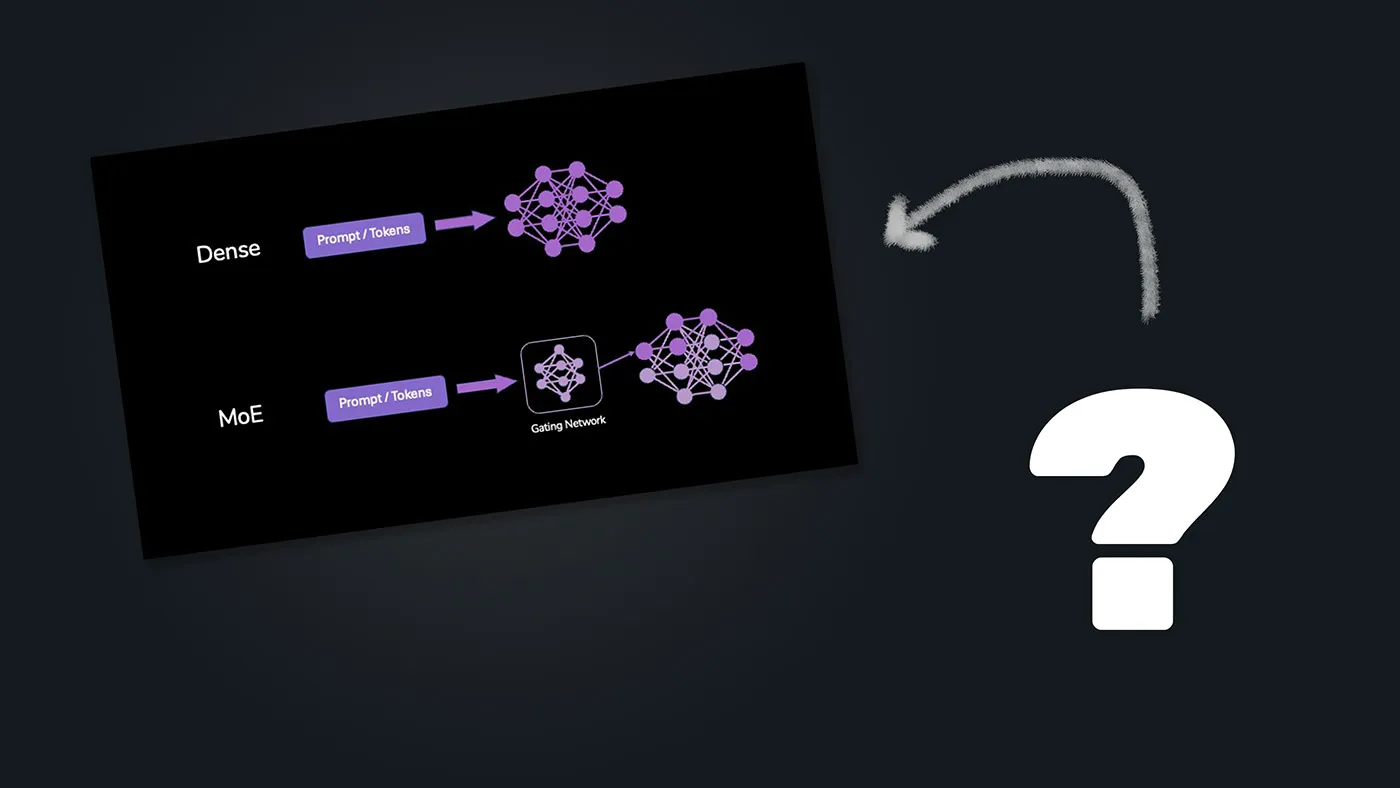
Mixture of Experts (MoE) vs Dense LLMs
When diving into open Large Language Models (LLMs) you can run locally, like the Gemma or Llama models, you’ll quickly encounter two main types: Dense models and Mixture of Experts (MoE) models.
For example, the Llama 4 models ( Scout and Maverick ) are MoE models, while the Llama 3 series is Dense.
It’s quite likely that you’ve probably used Dense models without even knowing it. But since MoE models are gaining traction, and their naming as well as memory requirements can be confusing, they’re worth a closer look.
So, what’s the difference, and what does it mean for you?

AI For Developers
Learn how to efficiently use GitHub Copilot, Cursor and ChatGPT to become a more productive developer.
What Are Dense LLMs?
Think of a “standard”, Dense LLM model like a single, highly knowledgeable expert (or team) that tackles every single part of your request with its full brainpower.
For every prompt that’s sent to the model, all model parameters are used to process the input and generate the output. This means that every single piece of data (token) is processed by the entire model, which can be computationally expensive.
It’s straightforward: more parameters generally (but not strictly) mean more knowledge and capability, but also more computation for every step.
Enter MoE: The Team of Specialists
Mixture of Experts (MoE) models take a different approach, inspired by the idea that sometimes, specialized knowledge is better.
Instead of one massive layer doing all the work, an MoE layer contains multiple smaller “expert” networks. Alongside these experts, there’s a “gating network” or “router.”
Here’s the clever part: When a token arrives at an MoE layer, the gating network quickly decides which expert(s) (often just one or two out of many) are best suited to handle that specific token.
Only the chosen experts get activated and perform calculations. The others remain inactive (for this request).
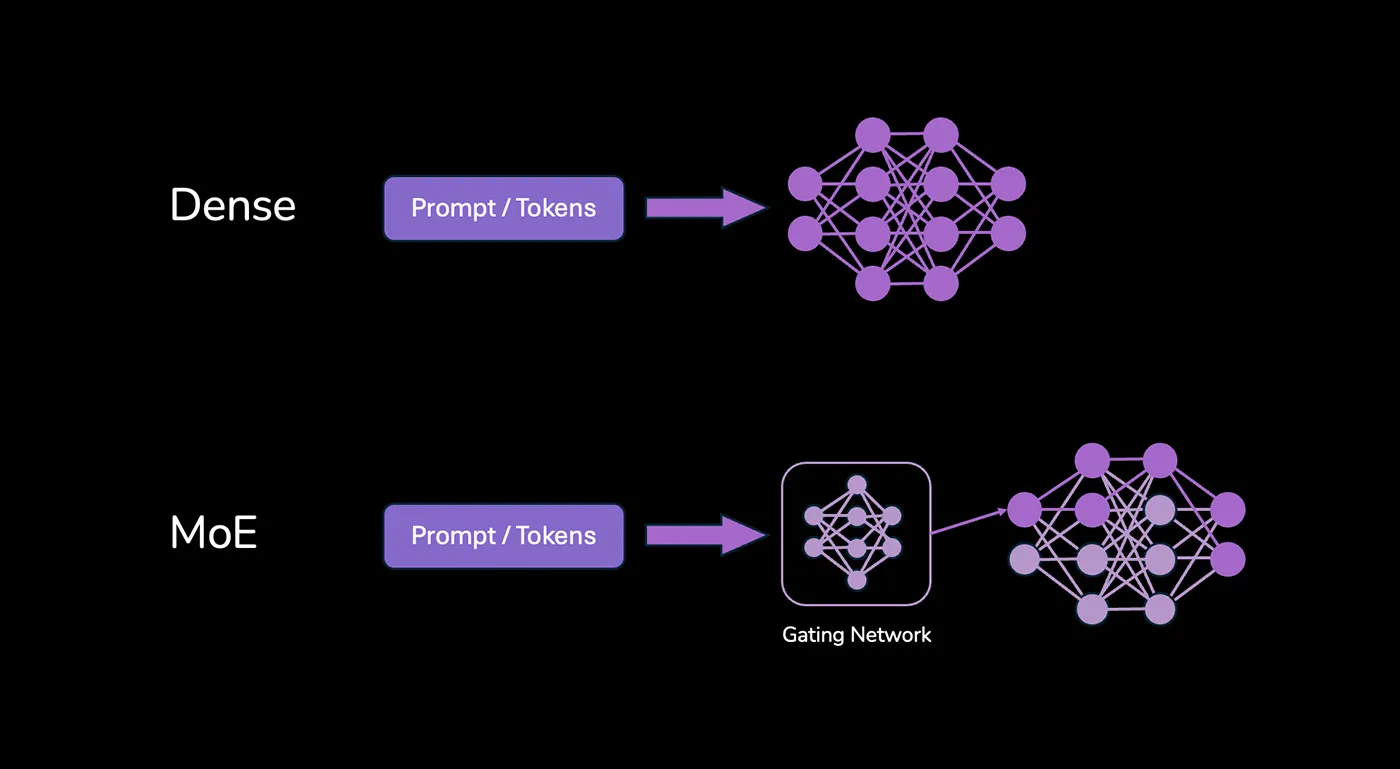
This is called sparse activation. The goal? To build models with a massive total number of parameters (representing vast knowledge) but only use a fraction of them for any given computation, thus saving on computational cost.
Models like Mixtral 8x7B (which has 8 experts) or Llama 4 Maverick (with 128 experts!) use this technique.
Are MoE Models Faster?
So … are MoE models faster? And better?
This is where things get interesting:
- Fewer Calculations: Yes, for a given token, an MoE model performs significantly fewer calculations (measured in FLOPs) than a Dense model of the same total parameter size. Llama 4 Maverick has a total amount of 400bn (!) parameters but “only” activates 17bn of those parameters for a given requeest. Its computational cost is therefore closer to a 17B dense model.
- Faster Inference (Usually): This computational saving often translates to faster inference speed (more tokens generated per second) compared to achieving the same quality/capability level with a hypothetical huge Dense model. It’s a way to get the benefits of scale without the full computational penalty.
- The Small Print: There’s a small overhead from the gating network deciding which expert to use. So, if you compare an MoE model to a Dense model that has the same number of active parameters, the MoE might be fractionally slower per token due to that routing step.
Imagine a complex task. A Dense model is like one genius trying to solve every single aspect. An MoE model is like a manager (the gate) quickly assigning sub-tasks to specialized experts.
The MoE approach can be faster overall for complex problems because specialists work efficiently, even if the initial assignment takes a moment.
Loading & Running Models Locally
Okay, MoE models are computationally cheaper per token for their size. That means they need less VRAM to run the calculations, right?
Wrong. Unfortunately.
This is the crucial catch for running models locally:
Both Dense AND MoE models typically require ALL their parameters to be loaded into your system’s RAM or GPU’s VRAM before you can start inference.
Why for MoE? Even though only a couple of experts are active for a specific token, the gating network needs access to all the experts to be able to choose the right ones dynamically.
Unfortunately, it’s not clear in advance, which of the total amount of parameters will become active for a given request. So they must all be loaded into (V)RAM upfront. The entire model, including all the inactive experts for that token, must reside in memory.
So, MoE models, despite their computational efficiency, can be extremely memory-hungry due to their large total parameter counts. A model like Llama 4 Maverick might only compute using 17B parameters at a time, but you need enough VRAM to hold its entire 400B parameter footprint (or a quantized version of it). This often pushes them out of reach for typical consumer hardware.
That’s why, for example, LM Studio (a great tool for running LLMs locally) shows me that the Llama 4 models (even the smaller Scout model) are out of reach for my M1 MacBook Pro system with 64GB of (unified) memory.
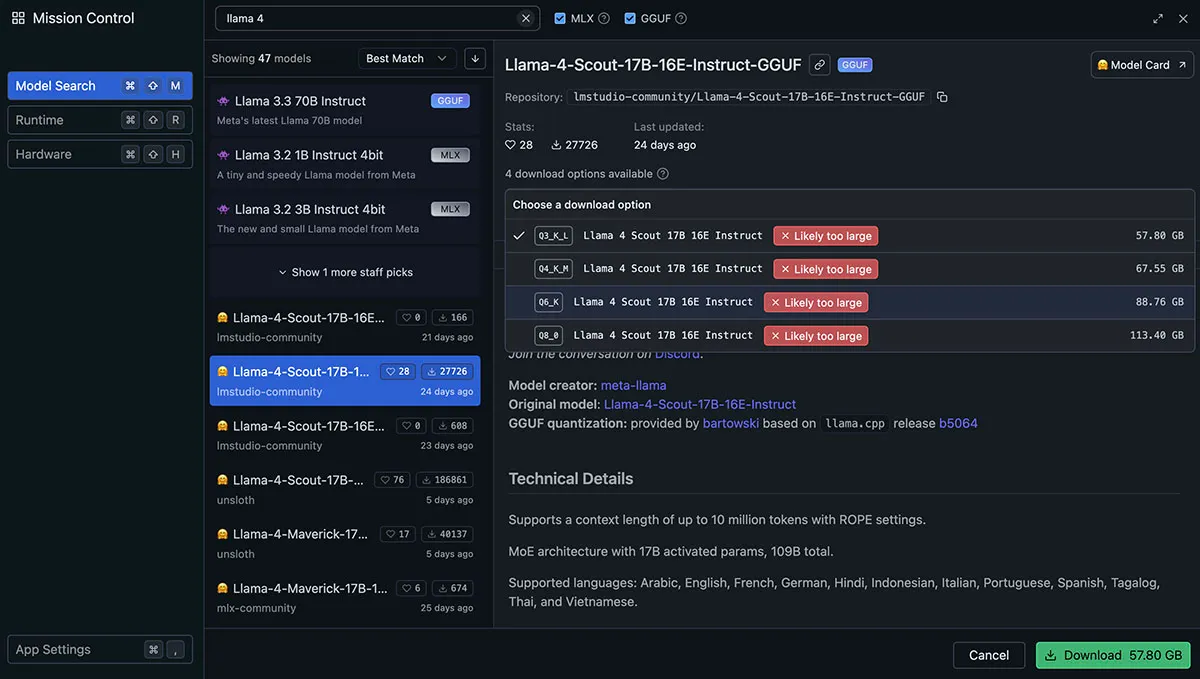
Especially when it comes to the Llama 4 models, Meta chose a quite confusing naming scheme since they put the number of active parameters in the model name (e.g., Llama 4 Maverick 17B).
That name “hides” the fact that the actual total parameter count is 400B.
That’s not a “hard rule” for MoE models, though - it’s a decision by Meta. For example, some of the new Qwen 3 models (e.g., the Qwen3-30B-A3B model) carry the total parameter count in their name (e.g., 30B).
So What’s Better?
Neither is universally “better” - they represent different design philosophies:
- Dense Models:
- Simpler architecture.
- Well-understood training and behavior.
- Memory requirements are directly linked to computational cost.
- Many excellent, highly optimized open models available (e.g., Gemma 3, some of the Qwen 3 models).
- MoE Models:
- Achieve high capability (knowledge) with lower computational cost per token (potentially faster inference for that capability).
- More complex architecture.
- Possibly very high memory requirements due to “hidden” large total parameter counts, making local use challenging.
- A growing trend for state-of-the-art open models (Mixtral, Llama 4, some Qwen 3 models).
MoE is a fascinating technique that allows AI models to scale to enormous sizes while keeping the computational cost of using them (inference) relatively manageable.
This often translates to faster performance compared to a dense model of similar overall capability.
However, MoE models still need all their parameters loaded into memory, which can be a significant limitation for local use (just as it can be a problem for big Dense models)
